Immutable Priority Queues
Dequeuing Values

Before we can start on the actual implementation of our immutable priority queue, we need to understand the algorithms we’re going to use. There are two different scenarios to consider - when we enqueue something onto the queue, and when we dequeue the head.

Removing an item from the queue is a simpler task, so let’s start by looking at the same heap we saw earlier:

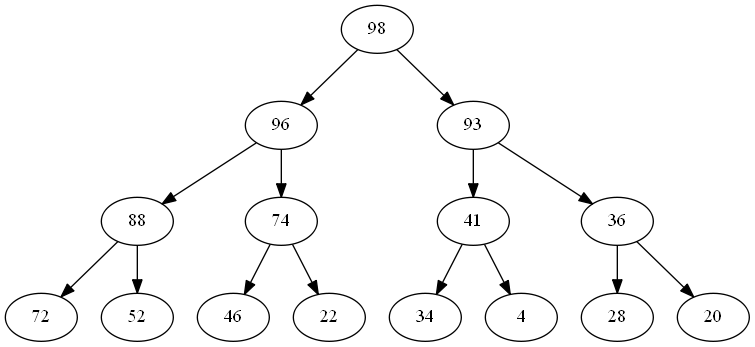
To dequeue the 98 from the root of the tree, here’s what happens:

• Removing the 98 from the root creates a gap that we fill by removing 96 from the root of the left branch (remember that the higher priority value will always be on the left).
• Promoting 96 to the root leaves a gap in the left subtree that we fill with 88 from its left subtree.
• Because 88 < 93, we swap the two branches under 96 so that 93 is on the left.
• Promoting 88 leaves a gap that we fill with 72.
• Because 72 < 74, we swap the two branches under 88 so that 74 is on the left.

We end up with a new heap that looks like this:

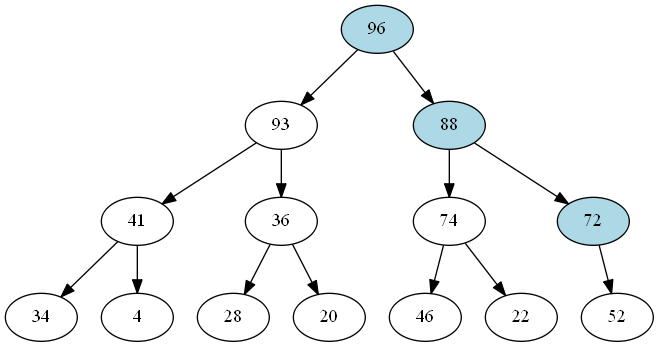
Remembering that we’re creating an immutable tree, we don’t modify any existing nodes - instead we create entirely new nodes as required. These new nodes are shown in the diagram above in blue.

Removing the 96 from the root of this tree follows a similar pattern:

• Removing the 96 from the root creates a gap that we fill using the 93 from the left branch.
• We promote 41 into the gap left vacant by 93, swapping the two branches so that 88 is on the left.
• Lastly, 34 is promoted into the gap left by 41.

We end up with this new heap:

As each value is removed, we promote the next contender from the left hand subtree; sometimes we need to swap the branches around to maintain our invariant that the greater value is on the left.

Here’s the result of removing 93 from the root of the above tree - see if you can follow the changes made.

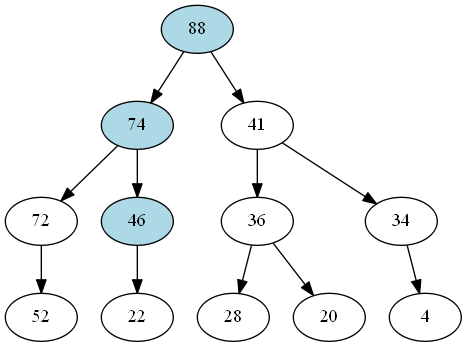
For all that it can be challenging to follow the transformation (it took me several attempts before the diagrams were correct!), the code to implement dequeue is actually a pretty simple recursive algorithm:

public IImmutablePriorityQueue<T> Dequeue()
{
    if (_left is SingleItemImmutablePriorityQueue<T> s)
    {
        return _right.Enqueue(_left.Head);
    }

    return new BranchingImmutablePriorityQueue<T>(
        _left.Head,
        _left.Dequeue(),
        _right,
        _comparer);
}

If the lefthand branch contains just a single node, we construct a new node by enqueing it into the righthand branch, otherwise we create a new branching node by removing head of the lefthand branch. We know we can do that because the largest branch item is always on the left - and we rely on the constructor to enforce that, swapping the branches if required.

Next time, we’ll look at the slightly more complicated process of enqueing values.