Immutable Priority Queues
Introducing the Priority Queue

Recently, while working on a personal project, I needed a priority queue. Instead of slamming all of the items into a sorted list and making do, I decided to do the job properly and write a proper abstraction. To keep things interesting, it was an immutable implementation.

What is a priority queue? A regular queue preserves the order of items - they are removed from the end of the queue in the same sequence that they were admitted to the queue originally. With a priority queue, an ordering function is used to reorder the items so that the most important items are removed from the queue first. Effectively, some items are fast-tracked and reach the front of the queue quickly, while others are held aside for later.

To implement this, we’ll use a data structure known as a heap - effectively a binary tree with a couple of simple additional rules:

• The highest priority item should always be at the root of any subtree
• When there are two branches off a node, the higher priority item should be on the left

Here’s an example:

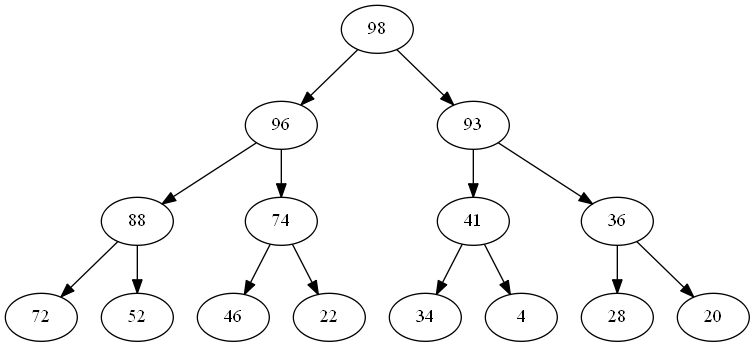
The highest priority item in the entire tree is the 98 found at the root.

Each of the subtrees also abides by this rule - check out how 96 is the greatest value in the left subtree, and 93 is the greatest value in the right subtree. The smaller subtrees also do this - look at how 88, 74, 41 and 36 are placed.

Observe also how the branches are arranged - in each case, the larger value is in the lefthand branch under a node. At the top, 96 is left of 93. Lower down, 88 is left of 74, 72 is left of 52, 41 is left of 36, and so on.

You can see how the simple rules are applied recursively to each subtree, giving a characteristic structure to the arrangement of nodes.

Writing the code to implement this tree is moderately straightforward - but as you might have guessed, we’ll encounter a few wrinkles as we go.