Immutable Priority Queues
Converting a List to a Queue

While chatting with a friend about this series, he made a suggestion about a significantly more effective way to implement the ToImmutablePriorityQueue extension method.

His observation stemmed from the way a linear list can be considered as an in-place binary heap, with the children of a given node located by index. If we start our indexes at zero, the tree forms like this:

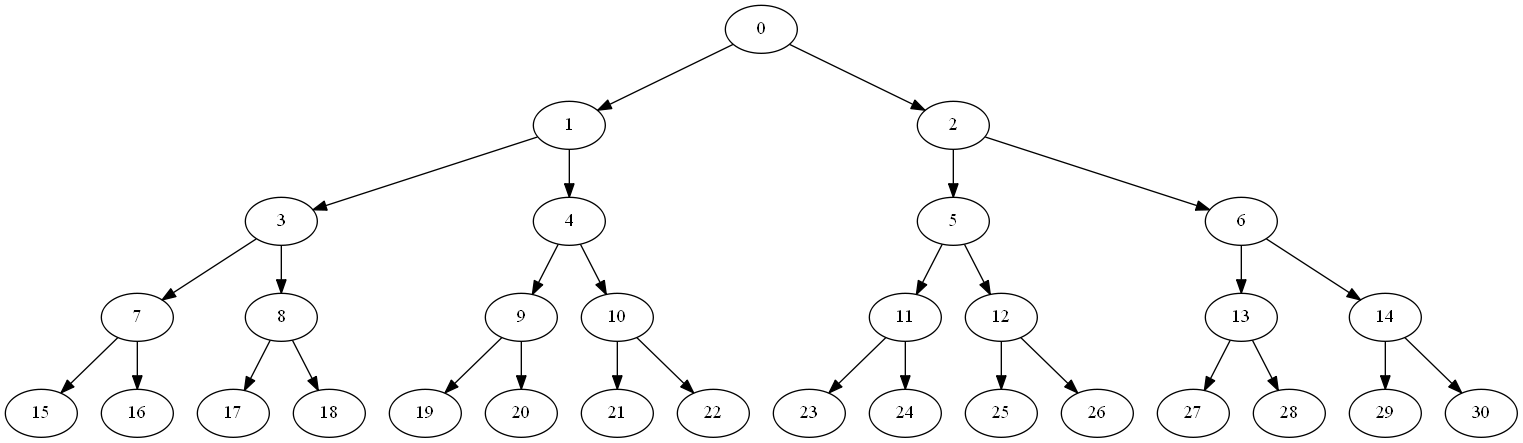
What we can do is use this relationship to directly create an immutable priority queue from a sorted list, bypassing all the heap debris and processing required by our earlier, naive approach.

There’s an obvious recursive implementation of this algorithm, but I decided instead on a straightforward implementation.

Here’s how the algorithm works:

• Sort all item items for our queue into order, with the highest priority items at the start of the list
• Iterate through the list in reverse order, starting with the lowest priority items at the end
• For each item, create an immutable priority queue instance
  • If the item has two child items, create a BranchingImmutablePriorityQueue
  • If the child has just one child item, create a DualItemImmutablePriorityQueue
  • Otherwise, as the item has no children, create a SingleItemImmutablePriorityQueue
• When finished, return the newly constructed queue at the head of the list.

Here’s the core method that does all the hard word:

public static IImmutablePriorityQueue<T> ToImmutablePriorityQueue<T>(
    this IEnumerable<T> items,
    Comparison<T> comparer)
{

To start, we scoop up all of items into a new list and sort it into the required order.

   var list = items.ToList();
    list.Sort(comparer);

Now we create a working stage to capture all our intermediate queue instances as we iterate.

    var stage = new IImmutablePriorityQueue<T>[list.Count];

    for (int index = list.Count - 1; index >= 0; index--)
    {
        var left = (index * 2) + 1;
        var right = left + 1;

We work out the indexes of the child items that might appear below this one. Based on whether both items exist, we take one of the following three branches.

        IImmutablePriorityQueue<T> queue;
        if (right < stage.Length)
        {
            queue = new BranchingImmutablePriorityQueue<T>(
                list[index],
                stage[left],
                stage[right],
                comparer);
        }
        else if (left < stage.Length)
        {
            queue = new DualItemImmutablePriorityQueue<T>(
                list[index],
                (SingleItemImmutablePriorityQueue<T>) stage[left],
                comparer);
        }
        else
        {
            queue = new SingleItemImmutablePriorityQueue<T>(
                list[index],
                comparer);
        }

        stage[index] = queue;
    }

Now we’ve finished working through the list, we can return the newly constructed queue.

    return stage[0];
}

Just as we have four different ways of creating empty queues, we need four different implementations of ToImmutablePriorityQueue<T>() to accommodate all the use cases. Fortunately these are all straightforward and can delegate most of the effort to this routine.

To test that the routine works as expected, we can write a simple property test to exercise it with a variety of inputs:

[Property]
public void ListConvertedToQueueReturnsExpectedItems(
    NonEmptyArray<string> values)
{
    var queue = values.Item.ToImmutablePriorityQueue(
        StringComparer.OrdinalIgnoreCase.Compare);
    var expected = values.Item.ToList();
    expected.Sort(StringComparer.OrdinalIgnoreCase.Compare);

    queue.Should().Equal(
        expected,
        StringComparer.OrdinalIgnoreCase.Equals);
}

The nice thing about this approach to list conversion is that it’s both faster (takes less time to execute) and smaller (doesn’t create very much in the way of heap debris).